Note
Go to the end to download the full example code.
Generating and Extracting Rotational Displacement#
In this example we show how to work with shells and rotation displacements.
Not all element types have rotational degrees of freedom, but generally, “shell” ones do. In this example we create a square shell with thickness of 0.1 and bend it, creating rotational displacement.
We subsequently plot the cumulative principal stresses and use
ansys.mapdl.core.inline_functions.Query to
extract the exact values of rotational displacement at the four corners
of our square.
# start MAPDL and enter the pre-processing routine
from ansys.mapdl.core import launch_mapdl
mapdl = launch_mapdl()
mapdl.prep7()
*****MAPDL VERIFICATION RUN ONLY*****
DO NOT USE RESULTS FOR PRODUCTION
***** MAPDL ANALYSIS DEFINITION (PREP7) *****
Mesh Setup#
In this example we create a simple 2D square, 1 x 1 in dimension, and give it the ‘SHELL181’ element type because this type has rotational degrees of freedom. Following this we:
Give the material an elastic modulus of 2e5 (EX)
Give the material a major poissons ratio of 0.3 (PRXY)
Set the section type to ‘SHELL’
Set the thickness to 0.1
Set the element size to 0.2
Mesh the square
Plot the mesh
mapdl.et(1, "SHELL181")
mapdl.mp("EX", 1, 2e5)
mapdl.mp("PRXY", 1, 0.3)
mapdl.rectng(0, 1, 0, 1)
mapdl.sectype(1, "SHELL")
mapdl.secdata(0.1)
mapdl.esize(0.2)
mapdl.amesh("all")
mapdl.eplot()

Applying Boundary Conditions#
Enter solution mode
Set analysis type to ‘STATIC’
Remove all degrees of freedom for nodes at
x = 0Apply a displacement of
uz = -0.1atx = 1Select all nodes
Solve the model
mapdl.run("/SOLU")
mapdl.antype("STATIC")
mapdl.nsel("s", "loc", "x", 0)
mapdl.d("all", "all")
mapdl.nsel("s", "loc", "x", 1)
mapdl.d("all", "uz", -0.1)
mapdl.allsel("all")
mapdl.solve()
***** MAPDL SOLVE COMMAND *****
*** NOTE *** CP = 0.000 TIME= 00:00:00
There is no title defined for this analysis.
*** SELECTION OF ELEMENT TECHNOLOGIES FOR APPLICABLE ELEMENTS ***
---GIVE SUGGESTIONS ONLY---
ELEMENT TYPE 1 IS SHELL181. IT IS ASSOCIATED WITH ELASTOPLASTIC
MATERIALS ONLY. KEYOPT(8)=2 IS SUGGESTED AND KEYOPT(3)=2 IS SUGGESTED FOR
HIGHER ACCURACY OF MEMBRANE STRESSES; OTHERWISE, KEYOPT(3)=0 IS SUGGESTED.
*****MAPDL VERIFICATION RUN ONLY*****
DO NOT USE RESULTS FOR PRODUCTION
S O L U T I O N O P T I O N S
PROBLEM DIMENSIONALITY. . . . . . . . . . . . .3-D
DEGREES OF FREEDOM. . . . . . UX UY UZ ROTX ROTY ROTZ
ANALYSIS TYPE . . . . . . . . . . . . . . . . .STATIC (STEADY-STATE)
GLOBALLY ASSEMBLED MATRIX . . . . . . . . . . .SYMMETRIC
*** NOTE *** CP = 0.000 TIME= 00:00:00
Present time 0 is less than or equal to the previous time. Time will
default to 1.
*** NOTE *** CP = 0.000 TIME= 00:00:00
The conditions for direct assembly have been met. No .emat or .erot
files will be produced.
D I S T R I B U T E D D O M A I N D E C O M P O S E R
...Number of elements: 25
...Number of nodes: 36
...Decompose to 0 CPU domains
...Element load balance ratio = 0.000
L O A D S T E P O P T I O N S
LOAD STEP NUMBER. . . . . . . . . . . . . . . . 1
TIME AT END OF THE LOAD STEP. . . . . . . . . . 1.0000
NUMBER OF SUBSTEPS. . . . . . . . . . . . . . . 1
STEP CHANGE BOUNDARY CONDITIONS . . . . . . . . NO
PRINT OUTPUT CONTROLS . . . . . . . . . . . . .NO PRINTOUT
DATABASE OUTPUT CONTROLS. . . . . . . . . . . .ALL DATA WRITTEN
FOR THE LAST SUBSTEP
*** NOTE *** CP = 0.000 TIME= 00:00:00
Predictor is ON by default for structural elements with rotational
degrees of freedom. Use the PRED,OFF command to turn the predictor
OFF if it adversely affects the convergence.
Range of element maximum matrix coefficients in global coordinates
Maximum = 7487.02512 at element 0.
Minimum = 7487.02512 at element 0.
*** ELEMENT MATRIX FORMULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
Time at end of element matrix formulation CP = 0.
DISTRIBUTED SPARSE MATRIX DIRECT SOLVER.
Number of equations = 174, Maximum wavefront = 0
Memory available (MB) = 0.0 , Memory required (MB) = 0.0
Distributed sparse solver maximum pivot= 0 at node 0 .
Distributed sparse solver minimum pivot= 0 at node 0 .
Distributed sparse solver minimum pivot in absolute value= 0 at node 0
.
*** ELEMENT RESULT CALCULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
*** NODAL LOAD CALCULATION TIMES
TYPE NUMBER ENAME TOTAL CP AVE CP
1 25 SHELL181 0.000 0.000000
*** LOAD STEP 1 SUBSTEP 1 COMPLETED. CUM ITER = 1
*** TIME = 1.00000 TIME INC = 1.00000 NEW TRIANG MATRIX
Plotting Stresses#
Extract the results
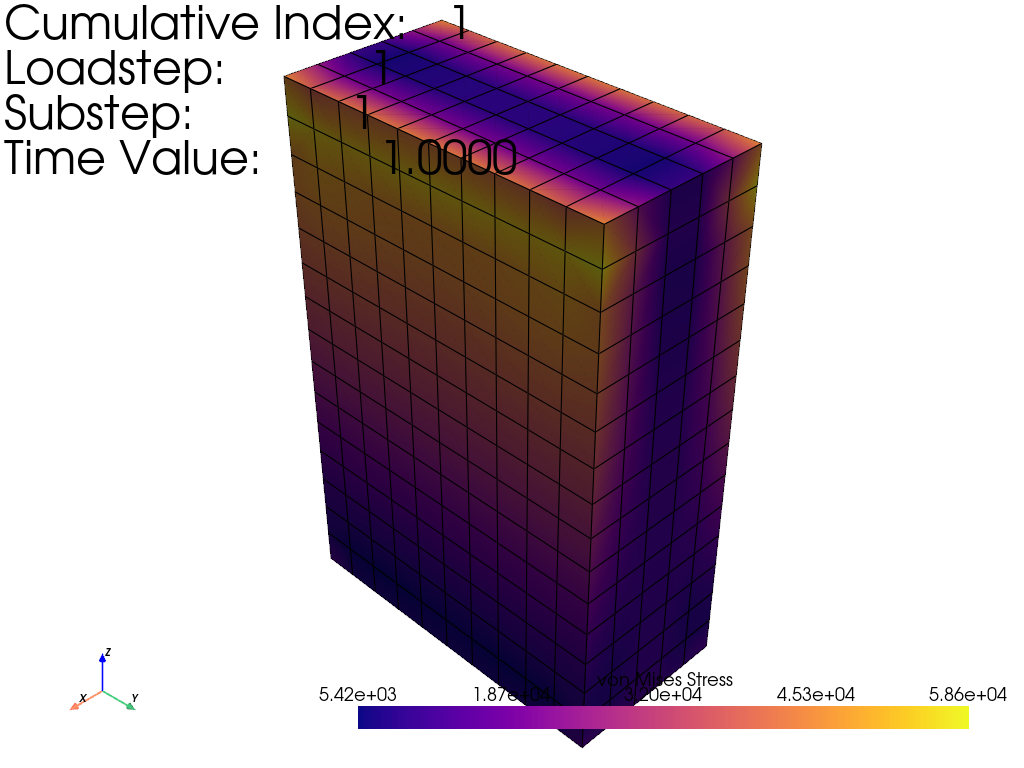
Plot the cumulative (0) equivalent stress (SEQV) - Set the colormap to ‘plasma’ because it is perceptually uniform - Show displacement so that we can see any deformation
result = mapdl.result
result.plot_principal_nodal_stress(
0, "SEQV", show_edges=True, cmap="plasma", show_displacement=True
)
Extracting Rotational Displacements#
Get a
ansys.mapdl.core.inline_functions.Queryinstance from thequeriespropertyLocate the nodes at the four corners of the square
Extract all 3 rotational displacement components for each one
Print them all
q = mapdl.queries
node1 = q.node(0, 0, 0)
node2 = q.node(0, 1, 0)
node3 = q.node(1, 0, 0)
node4 = q.node(1, 1, 0)
nodes = [node1, node2, node3, node4]
rotations = [(q.rotx(n), q.roty(n), q.rotz(n)) for n in nodes]
message = f"""
(0,1) B _________ C (1,1)
| |
| |
| |
|_________|
(0,0) A D (1,0)
N | (x_rot_disp, y_rot_disp, z_rot_disp)
--|------------------------------------
A | {rotations[0][0]:11.6f},{rotations[0][1]:11.6f},{rotations[0][2]:11.6f}
B | {rotations[1][0]:11.6f},{rotations[1][1]:11.6f},{rotations[1][2]:11.6f}
C | {rotations[2][0]:11.6f},{rotations[2][1]:11.6f},{rotations[2][2]:11.6f}
D | {rotations[3][0]:11.6f},{rotations[3][1]:11.6f},{rotations[3][2]:11.6f}
"""
print(message)
(0,1) B _________ C (1,1)
| |
| |
| |
|_________|
(0,0) A D (1,0)
N | (x_rot_disp, y_rot_disp, z_rot_disp)
--|------------------------------------
A | 0.000000, 0.000000, 0.000000
B | 0.000000, 0.000000, 0.000000
C | -0.000996, 0.155360, 0.000000
D | 0.000996, 0.155360, 0.000000
Stop mapdl#
mapdl.exit()
Total running time of the script: (0 minutes 1.133 seconds)

