Basic Thermal Analysis with PyMAPDL

This example demonstrates how you can use MAPDL to create a plate, impose thermal boundary conditions, solve, and plot it all within PyMAPDL.

First, start MAPDL as a service and disable all but error messages.

from ansys.mapdl.core import launch_mapdl

mapdl = launch_mapdl()

Geometry and Material Properties

Create a simple beam, specify the material properties, and mesh it.

mapdl.prep7()
mapdl.mp("kxx", 1, 45)
mapdl.et(1, 90)
mapdl.block(-0.3, 0.3, -0.46, 1.34, -0.2, -0.2 + 0.02)
mapdl.vsweep(1)
mapdl.eplot()

Boundary Conditions

Set the thermal boundary conditions

mapdl.asel("S", vmin=3)
mapdl.nsla()
mapdl.d("all", "temp", 5)
mapdl.asel("S", vmin=4)
mapdl.nsla()
mapdl.d("all", "temp", 100)
out = mapdl.allsel()

Solve

Solve the thermal static analysis and print the results

mapdl.vsweep(1)
mapdl.run("/SOLU")
print(mapdl.solve())
out = mapdl.finish()

*****  MAPDL SOLVE    COMMAND  *****

 *** NOTE ***                            CP =       0.000   TIME= 00:00:00
 There is no title defined for this analysis.
   *****MAPDL VERIFICATION RUN ONLY*****
     DO NOT USE RESULTS FOR PRODUCTION

                       S O L U T I O N   O P T I O N S

   PROBLEM DIMENSIONALITY. . . . . . . . . . . . .3-D
   DEGREES OF FREEDOM. . . . . . TEMP
   ANALYSIS TYPE . . . . . . . . . . . . . . . . .STATIC (STEADY-STATE)
   GLOBALLY ASSEMBLED MATRIX . . . . . . . . . . .SYMMETRIC

 *** NOTE ***                            CP =       0.000   TIME= 00:00:00
 Present time 0 is less than or equal to the previous time.  Time will
 default to 1.

 *** NOTE ***                            CP =       0.000   TIME= 00:00:00
 The conditions for direct assembly have been met.  No .emat or .erot
 files will be produced.



     D I S T R I B U T E D   D O M A I N   D E C O M P O S E R

  ...Number of elements: 450
  ...Number of nodes:    2720
  ...Decompose to 0 CPU domains
  ...Element load balance ratio =     0.000


                      L O A D   S T E P   O P T I O N S

   LOAD STEP NUMBER. . . . . . . . . . . . . . . .     1
   TIME AT END OF THE LOAD STEP. . . . . . . . . .  1.0000
   NUMBER OF SUBSTEPS. . . . . . . . . . . . . . .     1
   STEP CHANGE BOUNDARY CONDITIONS . . . . . . . .    NO
   PRINT OUTPUT CONTROLS . . . . . . . . . . . . .NO PRINTOUT
   DATABASE OUTPUT CONTROLS. . . . . . . . . . . .ALL DATA WRITTEN
                                                  FOR THE LAST SUBSTEP



 Range of element maximum matrix coefficients in global coordinates
 Maximum = 13.6474747 at element 0.
 Minimum = 13.6474747 at element 0.

   *** ELEMENT MATRIX FORMULATION TIMES
     TYPE    NUMBER   ENAME      TOTAL CP  AVE CP

        1       450  SOLID90       0.000   0.000000
 Time at end of element matrix formulation CP = 0.

 DISTRIBUTED SPARSE MATRIX DIRECT SOLVER.
  Number of equations =        2606,    Maximum wavefront =      0
  Memory available (MB) =    0.0    ,  Memory required (MB) =    0.0

 Distributed sparse solver maximum pivot= 0 at node 0 .
 Distributed sparse solver minimum pivot= 0 at node 0 .
 Distributed sparse solver minimum pivot in absolute value= 0 at node 0
 .

   *** ELEMENT RESULT CALCULATION TIMES
     TYPE    NUMBER   ENAME      TOTAL CP  AVE CP

        1       450  SOLID90       0.000   0.000000

   *** NODAL LOAD CALCULATION TIMES
     TYPE    NUMBER   ENAME      TOTAL CP  AVE CP

        1       450  SOLID90       0.000   0.000000
 *** LOAD STEP     1   SUBSTEP     1  COMPLETED.    CUM ITER =      1
 *** TIME =   1.00000         TIME INC =   1.00000      NEW TRIANG MATRIX

Post-Processing using MAPDL

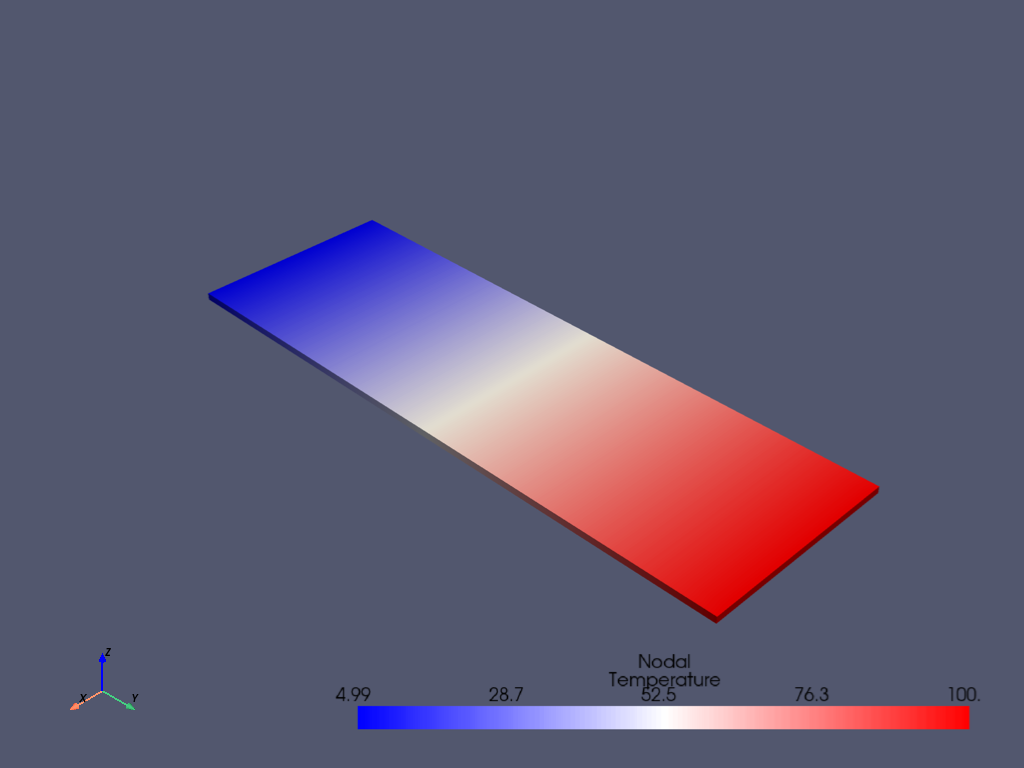
View the thermal solution of the beam by getting the results directly through MAPDL.

mapdl.post1()
mapdl.set(1, 1)
mapdl.post_processing.plot_nodal_temperature()

Alternatively you could also use the result object that reads in the result file using pyansys

result = mapdl.result
nnum, temp = result.nodal_temperature(0)
# this is the same as pyansys.read_binary(mapdl._result_file)
print(nnum, temp)

[    1     2     3 ... 11612 11613 11614] [ 0.  0.  0. ... nan nan nan]

Stop mapdl

mapdl.exit()