Path Operations within PyMAPDL and MAPDL

This tutorial shows how you can use pyansys and MAPDL to interpolate along a path for stress. This shows some advanced features of the pyvista module to perform the interpolation.

First, start MAPDL as a service and disable all but error messages.

import matplotlib.pyplot as plt
import numpy as np
import pyvista as pv

from ansys.mapdl.core import launch_mapdl

mapdl = launch_mapdl(loglevel="ERROR")

MAPDL: Solve a Beam with a Non-Uniform Load

Create a beam, apply a load, and solve for the static solution.

# beam dimensions
width_ = 0.5
height_ = 2
length_ = 10

# simple 3D beam
mapdl.clear()
mapdl.prep7()
mapdl.mp("EX", 1, 70000)
mapdl.mp("NUXY", 1, 0.3)
mapdl.csys(0)
mapdl.blc4(0, 0, 0.5, 2, length_)
mapdl.et(1, "SOLID186")
mapdl.type(1)
mapdl.keyopt(1, 2, 1)
mapdl.desize("", 100)

mapdl.vmesh("ALL")
# mapdl.eplot()

# fixed constraint
mapdl.nsel("s", "loc", "z", 0)
mapdl.d("all", "ux", 0)
mapdl.d("all", "uy", 0)
mapdl.d("all", "uz", 0)

# arbitrary non-uniform load
mapdl.nsel("s", "loc", "z", length_)
mapdl.f("all", "fz", 1)
mapdl.f("all", "fy", 10)
mapdl.nsel("r", "loc", "y", 0)
mapdl.f("all", "fx", 10)
mapdl.allsel()
mapdl.run("/solu")
sol_output = mapdl.solve()

# plot the normalized global displacement
mapdl.post_processing.plot_nodal_displacement(lighting=False, show_edges=True)

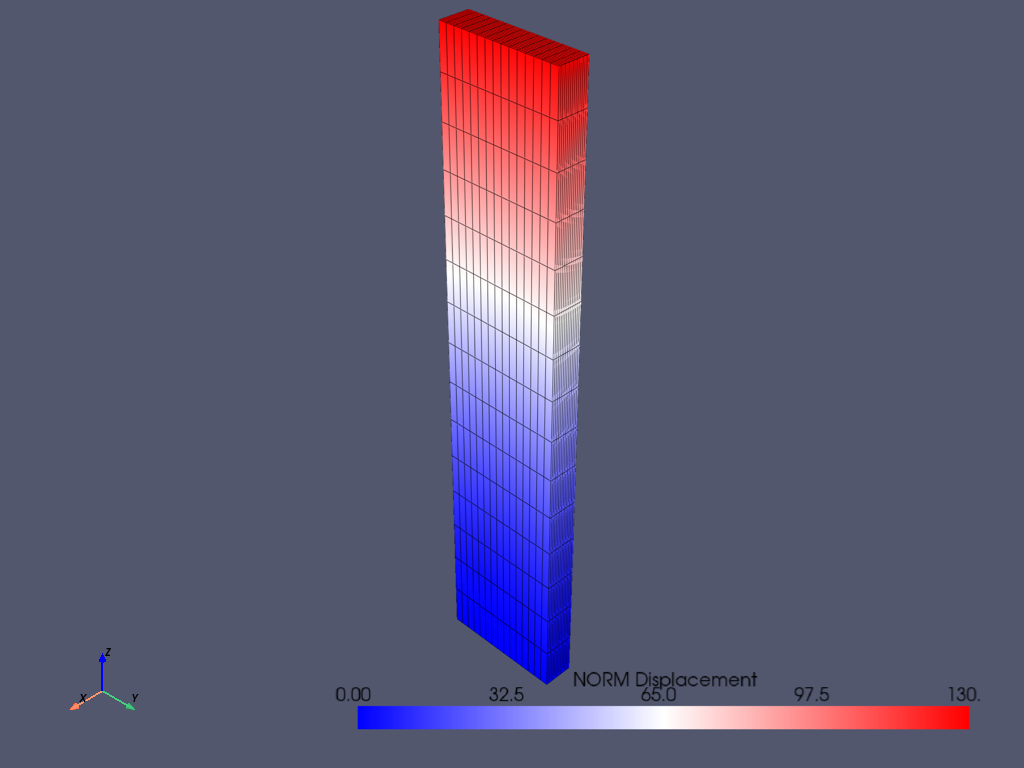
Post-Processing - MAPDL Path Operation

Compute the stress along a path within MAPDL and convert the result to a numpy array

mapdl.post1()
mapdl.set(1, 1)
# mapdl.plesol("s", "int")

# path definition
pl_end = (0.5 * width_, height_, 0.5 * length_)
pl_start = (0.5 * width_, 0, 0.5 * length_)

mapdl.run("width_ = %f" % width_)
mapdl.run("height_ = %f" % height_)
mapdl.run("length_ = %f" % length_)

mapdl.run("pl_end = node(0.5*width_, height_, 0.5*length_)")
mapdl.run("pl_start = node(0.5*width_, 0, 0.5*length_)")
mapdl.path("my_path", 2, ndiv=100)
mapdl.ppath(1, "pl_start")
mapdl.ppath(2, "pl_end")

# mapping components of interest to path.
mapdl.pdef("Sx_my_path", "s", "x")
mapdl.pdef("Sy_my_path", "s", "y")
mapdl.pdef("Sz_my_path", "s", "z")
mapdl.pdef("Sxy_my_path", "s", "xy")
mapdl.pdef("Syz_my_path", "s", "yz")
mapdl.pdef("Szx_my_path", "s", "xz")

# Extract the path results from MAPDL and send to a numpy array
nsigfig = 10
mapdl.header("OFF", "OFF", "OFF", "OFF", "OFF", "OFF")
mapdl.format("", "E", nsigfig + 9, nsigfig)
mapdl.page(1e9, "", -1, 240)

path_out = mapdl.prpath(
    "Sx_my_path",
    "Sy_my_path",
    "Sz_my_path",
    "Sxy_my_path",
    "Syz_my_path",
    "Szx_my_path",
)
table = np.genfromtxt(path_out.splitlines()[1:])
print("Numpy Array from MAPDL Shape:", table.shape)

Numpy Array from MAPDL Shape: (101, 7)

Comparing with Path Operation Within pyvista

The same path operation can be performed within pyvista by saving the resulting stress and storing within the underlying UnstructuredGrid

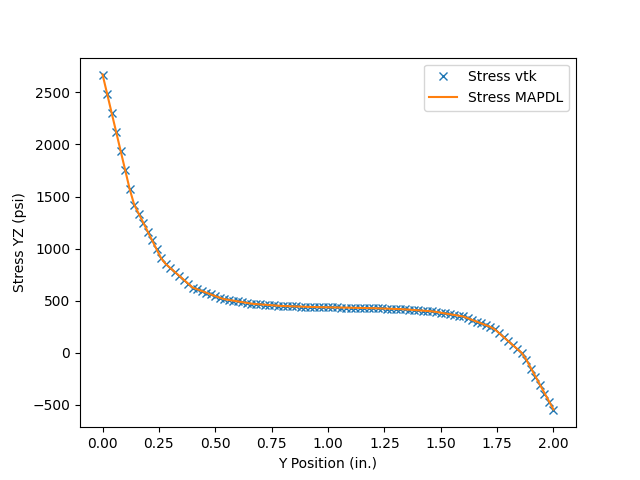
Take note that there is slight piece-wise behavior in both MAPDL’s and VTK’s interpoltion methods (both of which result in nearly identical interpolations). The underlying algorithm of VTK is:

The `vtkProbeFilter`, once it finds the cell containing a query
point, uses the cell's interpolation functions to perform the
interpolate / compute the point attributes.

# same thing in pyvista
rst = mapdl.result
nnum, stress = rst.nodal_stress(0)

# get SYZ stress
stress_yz = stress[:, 5]

# Assign the YZ stress to the underlying grid within the result instance.
# For this example, NAN values must be replaced with 0 for the
# interpolation to succeed
stress_yz[np.isnan(stress_yz)] = 0
rst.grid["Stress YZ"] = stress_yz

# Create a line and sample over it
line = pv.Line(pl_start, pl_end, resolution=100)
out = line.sample(rst.grid)  # bug where the interpolation must be run twice
out = line.sample(rst.grid)
# Note: We could have used a spline (or really, any dataset), and
# interpolated over it instead of a simple line.

# plot the interpolated stress from VTK and MAPDL
plt.plot(out.points[:, 1], out["Stress YZ"], "x", label="Stress vtk")
plt.plot(table[:, 0], table[:, 6], label="Stress MAPDL")
plt.legend()
plt.xlabel("Y Position (in.)")
plt.ylabel("Stress YZ (psi)")
plt.show()

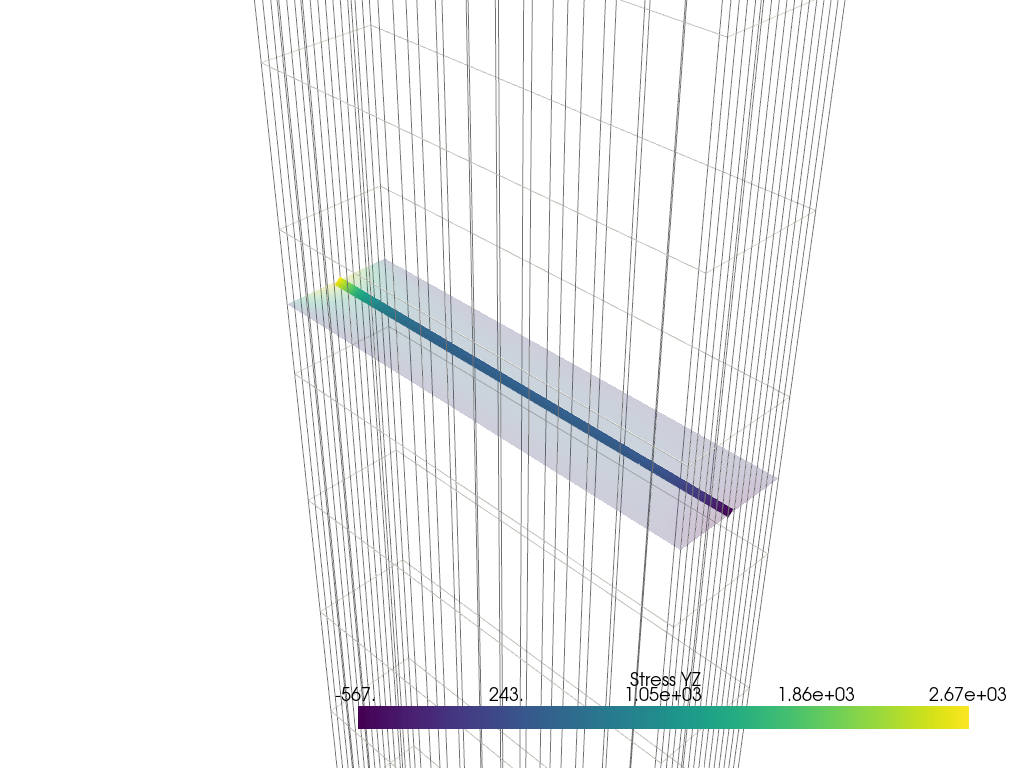
2D Slice Interpolation

Take a 2D slice along the beam and plot it alongside the stress at the line.

Note that this slice occurs between the edge nodes of this beam, necessitating interpolation as stress/strain is (in general) extrapolated to the edge nodes of ANSYS FEMs.

stress_slice = rst.grid.slice("z", pl_start)

# can plot this individually
# stress_slice.plot(scalars=stress_slice['Stress YZ'],
#                   scalar_bar_args={'title': 'Stress YZ'})

# good camera position (determined manually using pl.camera_position)
cpos = [(3.2, 4, 8), (0.25, 1.0, 5.0), (0.0, 0.0, 1.0)]
max_ = np.max((out["Stress YZ"].max(), stress_slice["Stress YZ"].max()))
min_ = np.min((out["Stress YZ"].min(), stress_slice["Stress YZ"].min()))
clim = [min_, max_]

pl = pv.Plotter()
pl.add_mesh(
    out,
    scalars=out["Stress YZ"],
    line_width=10,
    clim=clim,
    scalar_bar_args={"title": "Stress YZ"},
)
pl.add_mesh(
    stress_slice,
    scalars="Stress YZ",
    opacity=0.25,
    clim=clim,
    show_scalar_bar=False,
)
pl.add_mesh(rst.grid, color="w", style="wireframe", show_scalar_bar=False)
pl.camera_position = cpos
_ = pl.show()

Stop mapdl

mapdl.exit()